Cuerpos geométricos

2º -
Matemáticas y Tecnología
4.1. Volumen de los cuerpos geométricos
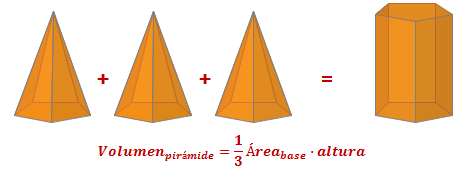
Volumen de pirámides y conos
|
Con una pirámide y un prisma con igual base y la misma altura podriamos realizar un sencillo experimento consistente en llenar de agua la pirámide, hasta arriba, y vaciarla en el prisma.
Puedes simular este experimento en la animación de la derecha y comprobar que el agua llena el prisma hasta la tercera parte de su altura. Para llenar el prisma necesitariamos vaciar el contenido de la pirámide tres veces.
|
|
Por tanto el volumen de la pirámide es la tercera parte del volumen del prisma que ya sabes calcular.
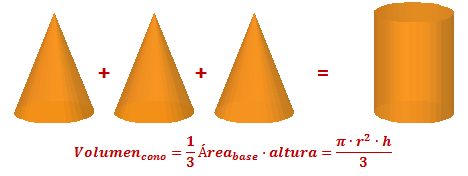
Lo mismo ocurre con los conos y cilindros, el volumen de un cono es la tercera parte del volumen de un cilindro con la misma base y altura.
EJEMPLOS
|
1) La pirámide de Giza es la mayor de las pirámides de Egipto que aún perdura, su base es un cuadrado de 230 m de lado y su altura mide 137 m. ¿Cuál es su volumen?
Área de la base = 230·230 = 52900 m²
Volumen = 52900·137/3 = 2415766,7 m³
|
|
2) ¿Cuántos cm³ de helado caben en un cono de 2,5 cm de radio y 15 cm de altura?
Área de la base = π·2,52 = 19,625 cm²
Volumen = 19,625·15/3 = 98,125 cm³
|
